excel 積分 やり方 数値を正確に積分するプロのテクニック
Excelを用いた数値積分の正確な方法について解説します。積分計算は、複雑な数式を扱う際に非常に有用なツールですが、正確な結果を得るためには特定のテクニックが必要です。本記事では、プロが実践するExcelでの積分計算のやり方を詳しく紹介します。数値データを正確に積分するための具体的な手順や、注意すべきポイントについても触れ、読者が実務で活用できる知識を提供します。Excelの機能を最大限に活用し、精度の高い積分結果を得る方法を学びましょう。
Excelで数値を正確に積分するためのプロフェッショナルなテクニック
Excelを使用して数値積分を行うことは、データ分析や科学計算の分野で非常に重要です。数値積分は、関数やデータセットの定積分を近似的に計算する手法であり、さまざまな工学や物理学の問題を解決するために不可欠です。
数値積分の基本原理
数値積分は、連続する関数やデータポイントを有限個の離散点に分割し、それらの点における関数値を使用して積分値を近似します。一般的な数値積分法には、台形公式やシンプソンの公式などがあります。これらの方法は、関数の曲線下面積を近似するために使用されます。 数値積分法を選択する際には、以下の点を考慮する必要があります。
- 精度:使用する方法がどの程度の精度を達成できるか。
- 計算コスト:計算に必要な時間やリソース。
- データの特性:データが滑らかであるか、または不連続点を含むか。
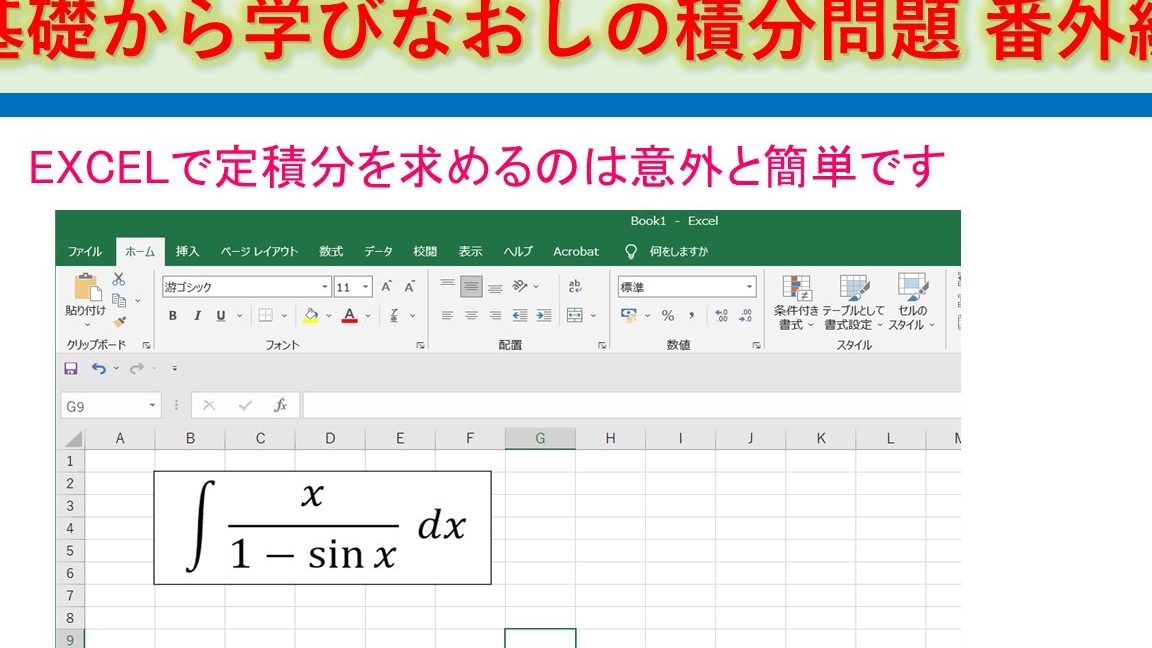
Excelでの数値積分のやり方
Excelで数値積分を実行するには、まずデータを適切に準備する必要があります。具体的には、x値と対応するy値を含むデータテーブルを作成します。次に、台形公式やシンプソンの公式を適用して積分を計算します。 ExcelのVBA(Visual Basic for Applications)を使用すると、数値積分の計算を自動化し、カスタマイズすることができます。VBAを使用することで、複雑な数値積分法を実装し、繰り返し計算を効率的に実行できます。
台形公式の適用
台形公式は、数値積分の最も基本的な方法の一つです。この方法では、データポイント間の領域を台形と見なし、それらの面積の合計を計算します。台形公式は比較的簡単に実装でき、多くの場合で良好な結果をもたらします。 台形公式の適用例:
- x値とy値のデータセットを準備します。
- 隣接するデータポイント間の幅(h)とy値の平均を計算します。
- 台形の面積(h yの平均)を計算し、合計します。
シンプソンの公式の適用
シンプソンの公式は、台形公式よりも高い精度を提供する数値積分法です。この方法では、データポイントを2次関数で近似し、その関数の下での面積を計算します。シンプソンの公式は、滑らかな関数に対して特に有効です。 シンプソンの公式を使用する際の注意点:
- データポイントの数が奇数である必要があります。
- データポイントが均等に間隔をあけている必要があります。
- 関数の2次導関数が大きい場合、精度が低下する可能性があります。
Excelでの数値積分の応用例
数値積分は、さまざまな分野で幅広く応用されています。例えば、物理学では、物体の運動エネルギーや位置エネルギーを計算するために使用されます。また、工学では、応力やひずみの解析に役立ちます。 Excelでの数値積分は、これらの計算を迅速かつ正確に実行する強力なツールとなります。適切な数値積分法を選択し、Excelの機能を活用することで、複雑な問題を効率的に解決できます。
詳細情報
エクセルで数値積分を行う基本的な方法とは?
エクセルで数値積分を行うには、主に台形公式やシンプソンの公式などの数値積分法が用いられます。これらの方法は、関数を一定の区間で分割し、各区間での面積を近似することで全体の積分値を計算します。特に、台形公式はシンプルで実装が容易なため、初心者にも扱いやすいです。
エクセルでの数値積分の精度を高めるには?
数値積分の精度を高めるためには、分割する区間の数を増やすことが有効です。区間を細かくすることで、関数の曲線をより正確に近似でき、結果として積分値の精度が向上します。また、適切な数値積分法を選択することも重要で、例えばシンプソンの公式は台形公式よりも一般的に高い精度を提供します。
エクセルで複雑な関数の数値積分を行う場合の注意点は?
複雑な関数の数値積分を行う場合、関数の性質を理解することが重要です。特に、不連続点や特異点を含む関数の場合、適切な処理を行わないと大きな誤差が生じる可能性があります。そのため、これらの点を避けるように区間を設定するか、特別な数値積分法を適用する必要があります。
エクセル以外のツールで数値積分を行う利点は?
エクセル以外のツール、例えばMATLABやPythonのライブラリ(SciPyなど)を使用すると、より高度な数値積分法を簡単に実装できます。これらのツールは、適応型数値積分法など、エクセルでは扱いにくい複雑な方法も提供しており、非常に高い精度での積分計算が可能です。