Excel最小二乗法でデータ分析をマスター
データ分析の世界では、正確な予測と洞察が求められます。そのためには、効果的な分析手法を身につけることが重要です。Excelの最小二乗法は、データ分析の基本的なツールであり、データの傾向を把握し、将来の予測を行うのに役立ちます。本記事では、Excelの最小二乗法を用いたデータ分析の方法を詳しく解説し、データ分析のスキルを高めるための具体的な手順を紹介します。最小二乗法の基礎から応用まで、実践的な知識を身につけましょう。
Excel最小二乗法の基本と応用
Excelの最小二乗法は、データ分析において非常に重要な役割を果たします。この手法を用いると、データの傾向を把握し、予測モデルを構築することができます。最小二乗法は、観測データと予測値の間の誤差を最小化するようにモデルを調整します。
最小二乗法の原理
最小二乗法は、回帰分析の基本的な手法であり、データの傾向を最もよく表す直線または曲線を見つけることを目的としています。この手法では、観測データと予測値の間の残差の二乗の合計を最小化します。具体的には、以下の式を用いて、回帰係数を推定します。
- 回帰直線の式を定義する
- 残差の二乗の合計を計算する
- 回帰係数を最適化する
Excelでの最小二乗法の実装
Excelでは、最小二乗法を用いた回帰分析を簡単に行うことができます。具体的には、以下の手順で行います。
- データ分析ツールを有効にする
- 回帰分析を実行する
- 回帰係数と決定係数を解釈する
最小二乗法の応用例
最小二乗法は、さまざまな分野で応用されています。たとえば、売上予測や市場分析など、データの傾向を把握する必要がある場合に有効です。また、科学研究においても、実験データの解析に用いられることがあります。
- 時系列データの分析
- 多変量解析への拡張
- 予測モデルの構築
最小二乗法の限界と課題
最小二乗法は強力な手法ですが、いくつかの限界と課題もあります。たとえば、外れ値の影響を受けやすいことや、多重共線性の問題などがあります。これらの問題に対処するには、ロバスト回帰や正則化などの手法を用いる必要があります。
- 外れ値の検出と処理
- 多重共線性の検出と対処
- モデルの検証
最小二乗法の実践的な活用
最小二乗法を実践的に活用するには、データの特性を理解し、適切なモデルを選択することが重要です。また、モデルの解釈と結果の検証も必要です。Excelを用いた最小二乗法の実装は、データ分析の入門者にとって非常に有用です。
詳細情報
Excelで最小二乗法を使用するメリットは何ですか?
データ分析の精度を高めるために、Excelの最小二乗法は非常に有効なツールです。この手法を使用することで、回帰分析の結果を簡単に取得でき、データの傾向を把握することができます。
最小二乗法で使用するデータの条件は何ですか?
最小二乗法を使用する際には、データの独立性と正規分布が前提条件となります。また、外れ値の存在にも注意を払う必要があります。これらの条件を満たさない場合、分析結果の信頼性が低下する可能性があります。
Excelで最小二乗法を実施する手順を教えてください。
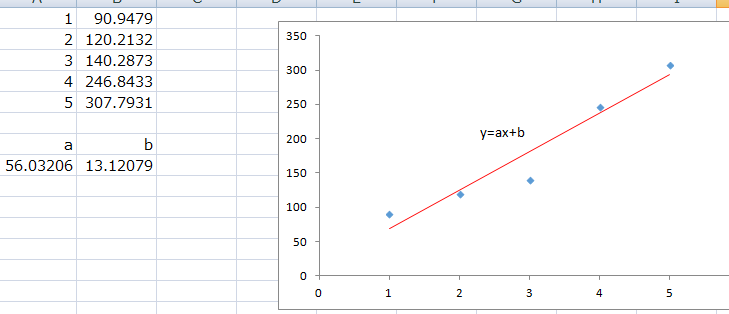
Excelで最小二乗法を実施するには、まずデータの入力とグラフの作成を行います。次に、回帰分析のツールを使用して、係数と決定係数を算出します。これらの値を基に、データの分析と解釈を行います。
最小二乗法の結果をどのように解釈しますか?
最小二乗法の結果は、回帰式と決定係数によって表されます。回帰式は、独立変数と従属変数の関係を示し、決定係数は、モデルの適合度を表します。これらの値を基に、データの傾向と要因を分析することができます。