最小二乗法Excelでデータ分析を簡単に
データ分析は、ビジネスや研究において重要な役割を果たしています。Excelは、データ分析のための強力なツールであり、最小二乗法はその中でも特に有用な手法の一つです。最小二乗法を使用すると、データの傾向を把握し、予測モデルを構築することができます。Excelでは、最小二乗法を簡単に実装でき、複雑な計算を自動化することができます。本記事では、最小二乗法の基本原理と、Excelでの実装方法について詳しく解説します。データ分析の効率化を目指す方々にとって、貴重な情報となるでしょう。最小二乗法の活用方法を学びましょう。
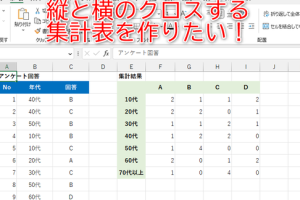
最小二乗法をExcelで活用するメリット
最小二乗法は、データ分析において非常に重要な手法であり、Excelを用いることで簡単に実行できる。Excelの機能を活用することで、複雑な計算を自動化し、データの傾向を把握することができる。
最小二乗法の基本概念
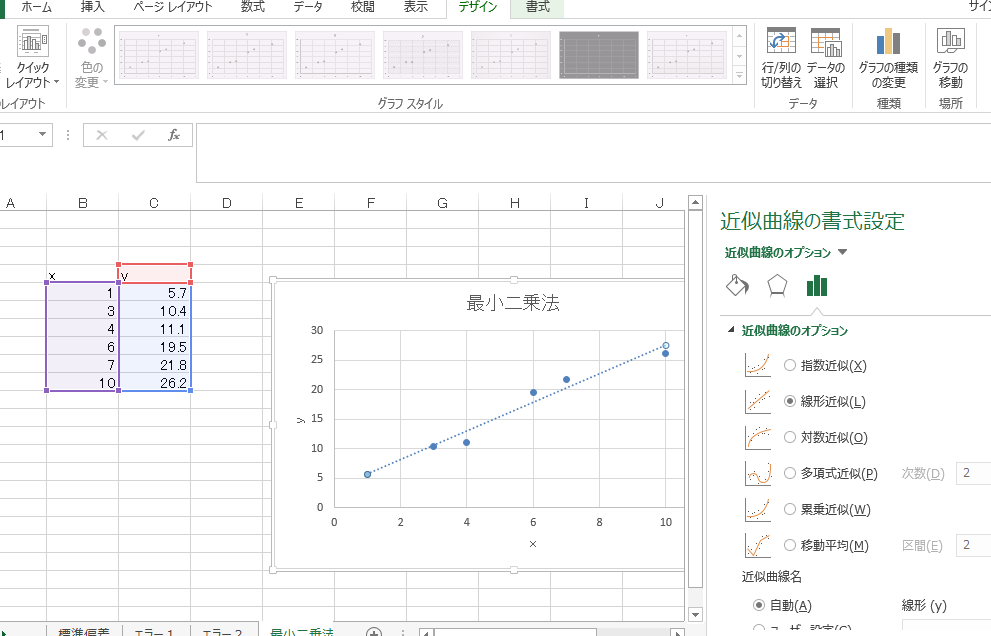
最小二乗法は、観測データに最もよく合うようなモデルを推定するための統計的手法である。この手法は、残差平方和を最小化することで、モデルのパラメータを決定する。Excelでは、回帰分析ツールを用いることで、簡単に最小二乗法を実行できる。 主な特徴は以下の通りである。
- データの傾向を把握できる
- 予測モデルの構築が可能である
- 分析の自動化が容易である
Excelでの最小二乗法の実行方法
Excelで最小二乗法を実行するには、分析ツールを有効にする必要がある。分析ツールを有効にした後、回帰分析を実行することで、最小二乗法によるデータ分析が可能になる。 実行手順は以下の通りである。
- 分析ツールを有効にする
- データ分析を選択する
- 回帰分析を実行する
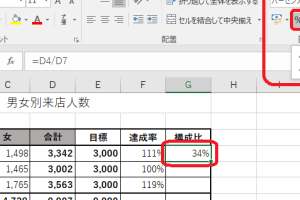
最小二乗法の結果の解釈
最小二乗法の結果は、回帰係数や決定係数などを含む。回帰係数は、独立変数と従属変数の関係を示し、決定係数は、モデルの適合度を示す。 結果の解釈は以下の通りである。
- 回帰係数の値を調べる
- 決定係数の値を調べる
- 残差の分布を確認する
最小二乗法の応用例
最小二乗法は、さまざまな分野で応用されている。例えば、売上予測や市場分析などに利用される。 応用例は以下の通りである。
- 売上予測モデルを構築する
- 市場分析を行う
- リスク分析を実施する
最小二乗法の限界
最小二乗法には、いくつかの限界がある。例えば、多重共線性や異常値の影響を受けることがある。 限界は以下の通りである。
- 多重共線性の問題
- 異常値の影響
- モデル選択の重要性
詳細情報
最小二乗法とは何ですか?
最小二乗法は、データ分析において予測値と実測値の間の誤差を最小化するための手法です。この方法は、回帰分析でよく使用され、最適なモデルを構築するために役立ちます。
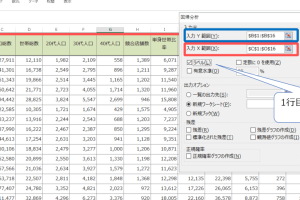
Excelで最小二乗法を使用する方法は?
Excelでは、データ分析ツールを使用して最小二乗法を簡単に適用できます。具体的には、回帰分析ツールを選んで、入力範囲と出力範囲を指定することで、回帰係数や決定係数を算出できます。
最小二乗法の利点は何ですか?
最小二乗法の主な利点は、データの傾向を簡潔に把握できることです。また、予測モデルを構築する際に、パラメータを最適化するために使用できます。これにより、正確な予測が可能になります。
最小二乗法を使用する際の注意点は?
最小二乗法を使用する際には、データの質とモデルの仮定に注意する必要があります。特に、外れ値や多重共線性の問題に対処する必要があります。これらに対処することで、信頼性の高い結果を得ることができます。